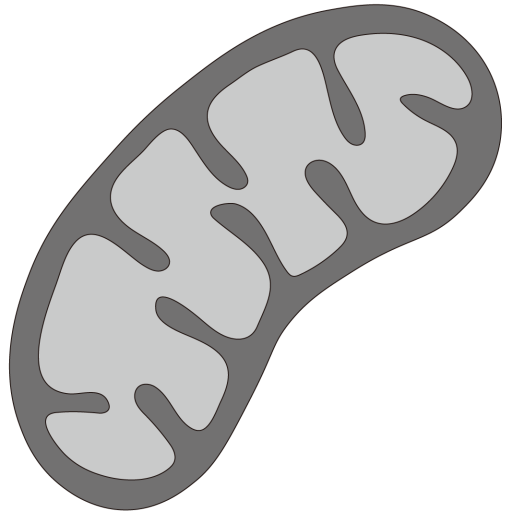
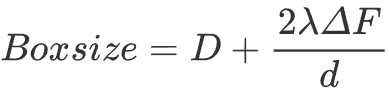图c是一个经过CTF校正之后的对齐的颗粒平均,图d对它模拟了2.2 μm的欠焦,可以看到周围扩散的波纹,这展示了欠焦对于颗粒的影响,欠焦使得信号产生了偏移。
CTF也可以理解为对这种图像扩散的数学函数的傅里叶变换。
如果要保留这个颗粒的这些高分辨信息,就需要比颗粒直径更大的Box size,来捕捉所有属于这个颗粒的信号。
Reference: Fred J. Sigworth. Microscopy, 65 (1):57–67. 2016
根据Peter B. Rosenthal和Richard Henderson的理论,由于欠焦引起信号偏移,建议的Box size为:
-
D是真实颗粒直径
-
λ 是电子波长
-
ΔF是欠焦值
-
d是期望保留高分辨率信息
Reference: Peter B. Rosenthal & Richard Henderson. Journal of Molecular Biology 333 (41):721-754. 2003
300 kV透射电镜下电子波长为0.0197 Å。假设欠焦为1 μm,期望分辨率为3 Å,那么
理论建议的Box size为:2×0.0197×10000/3 ≈ 131。要取一个比颗粒直径大131Å左右的Box size,才能获得足够高分辨信息用于重构。
这只是理论值,更大的Box size会增加计算时间、运算成本和存储的压力,所以综合考虑选取一个合适的大小很重要。
通常的经验值取颗粒大小的125%-200%可能是一个比较好的初始尝试。
注意换算单位,数据处理软件的提取Box size通常单位都是pixel。
还有一个要注意的是,由于现在主流的软件算法中傅里叶变换用的都是快速傅里叶变换算法(FFT),如果 Box size 是2的幂,FFT算法可以达到最优的效率。所以这个也是一个重要的考虑因素,常常128、256、512这种都是比较好的box size。